DAN LOK VAULT
“A Rare Opportunity To Own Dan Lok’s Lifetime Work and Unlock Your Wealth – All In One Go!”
This exclusive collection is everything you need to recession-proof your life – even when the world economy is on its knees.
Dan always talks about how important it is to have multiple High-Income Skills. That’s because having good High-Income Skills was the only way he got out of $150K of debt to become the successful entrepreneur he is today. It’s one of the fastest ways to earn a good income when you’re starting from scratch. Or to accelerate an existing business, you have to take it to the next level!
So whether you want to scale your business today, or you just want to increase your income-cap, this bundle can help you with both.
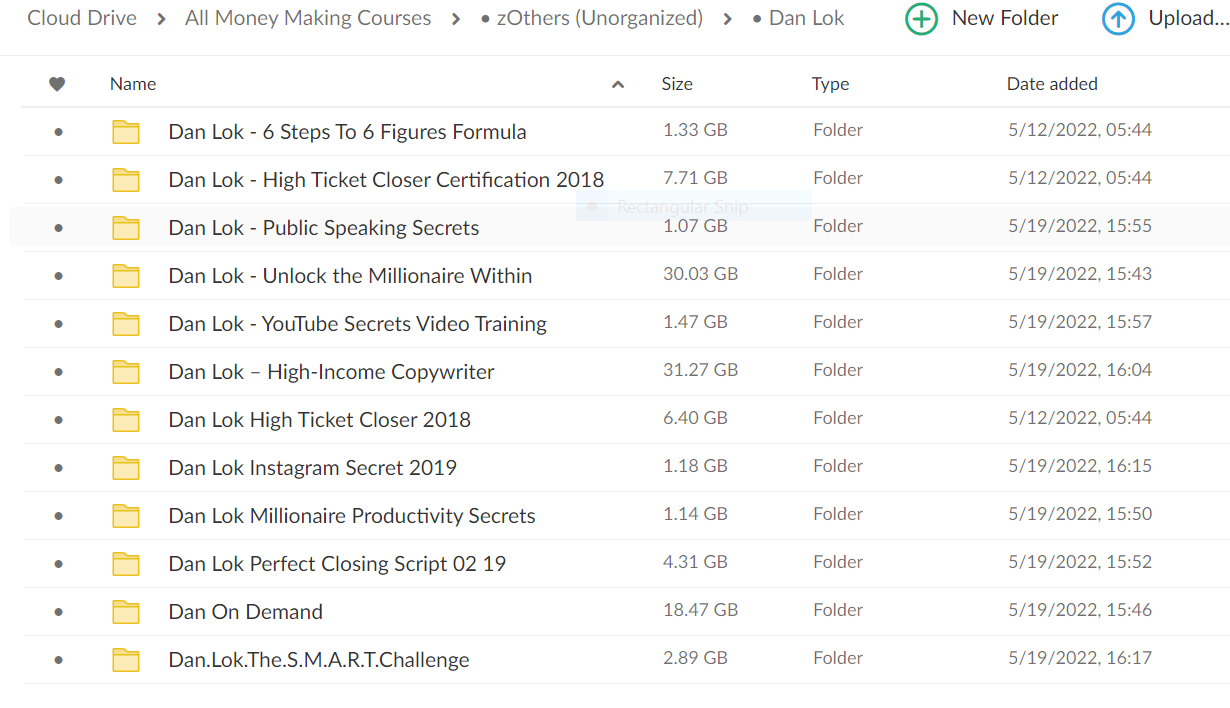
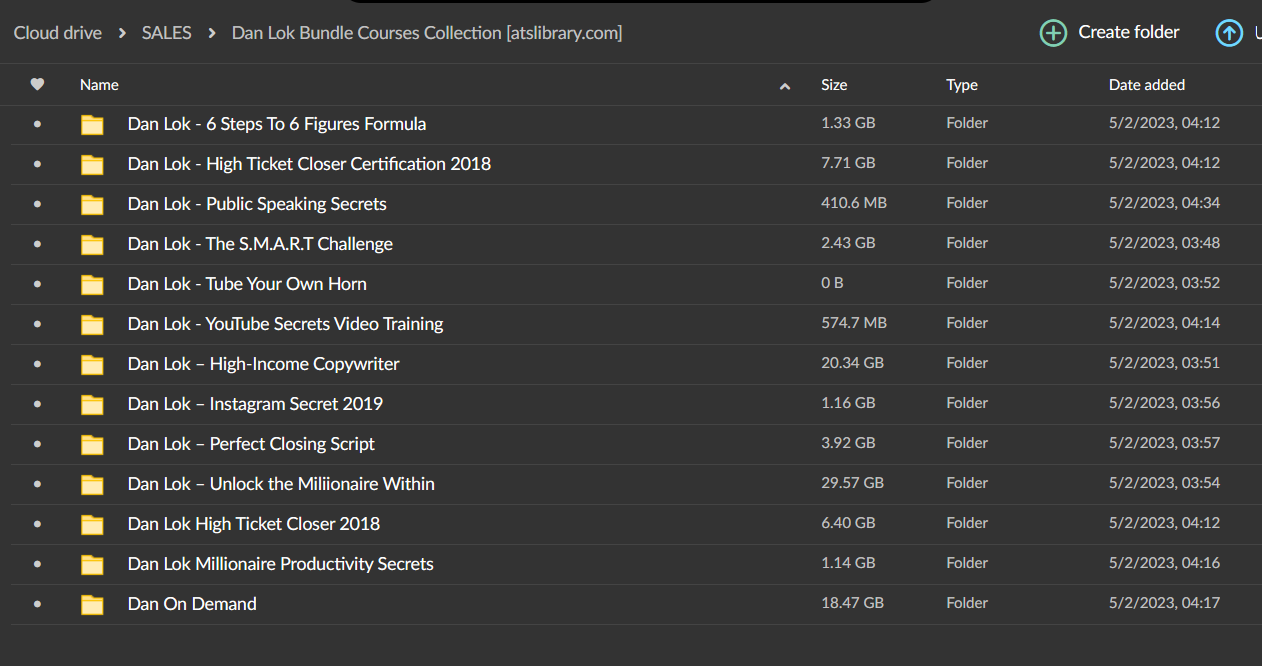
This Bundle Contain:
- Dan Lok – 6 Steps To 6 Figures Formula (1.32GB)
- Dan Lok – High Ticket Closer Certification Updated (7.71GB)
- Dan Lok – Public Speaking Secrets (1.07GB)
- Dan Lok – Unlock the Millionaire Within (30.03GB)
- Dan Lok – YouTube Secrets Video Training (1.47GB)
- Dan Lok – High-Income Copywriter (31.27GB)
- Dan Lok High Ticket Closer Updated (6.40GB)
- Dan Lok Instagram Secret Updated (1.18GB)
- Dan Lok Millionaire Productivity Secrets (1.14GB)
- Dan Lok Perfect Closing Script Updated (4.31GB)
- Dan On Demand 2022 Updated(18.47GB)
- Dan Lok – The S.M.A.R.T. Challenge (2.89GB)
TOTAL SIZE= 107.26GB
Course Updated 2023 (swipe left to check newly added prove)


 Over 1.000 comments
Over 1.000 comments